Kubin

• Strona główna • Moje rzeczy • Kartki • Esoterica • Kontakt •

Fenwick tree, best tree

Wprowadzenie

Weźmy sobie pewną operację \( a \circ b \). Ma ona spełniać następujące własności:

Takie operacje są dosyć naturalne. Parę przykładów:

Na pewnym ciągu \( a = (a_1, a_2, ..., a_n) \) chcemy wykonywać następujące operacje:

  1. Zapytanie. Dla podanych \( (l, r) \), zwróć \( a_l \circ a_{l+1} \circ \dots \circ a_r \).
  2. Modyfikacja. Dla podanych \( (i, d) \), wykonaj \( a_i := a_i + d \).
Oczywiście, taki problem bardzo łatwo można rozwiązać za pomocą drzewa przedziałowego. Jednak można to zrobić o wiele łatwiej za pomocą drzewa Fenwicka (alternatywnie nazywanego drzewem potęgowym, po angielsku Fenwick tree bądź Binary Indexed Tree [BIT]). Osiągniemy w bardzo prosty sposób złożoność \( O(\log n) \) na obie operacje.

Idea

Drzewo Fenwicka zwykle zakłada indeksowanie ciągu od jedynki, i tak też ja robię tutaj.

Idea drzewa Fenwicka jest bardzo prosta: aby realizować operacje, będziemy utrzymać pewną tablicę \(F = (F_1, F_2, ..., F_n) \). W \( F_i \) będziemy przechowywać wynik operacji \( \circ \) na przedziale \( \left( i - lsb(i), i \right] \) (czyli przedział kończący się w \( i \) o długości \( lsb(i) \)), gdzie \( lsb(i) \) to least significant bit, czyli najmniej znacząca jedynka w zapisie binarnym liczby \( i \). Przykładowo, \( lsb(84_{10}) = lsb(0101\ 0\color{red}{1}00_2) = 0000\ 0\color{red}{1}00 \).

Dziwne rzeczy na bitach

Tak wyglądają zakresy obejmowane przez kolejne komórki \( F \):

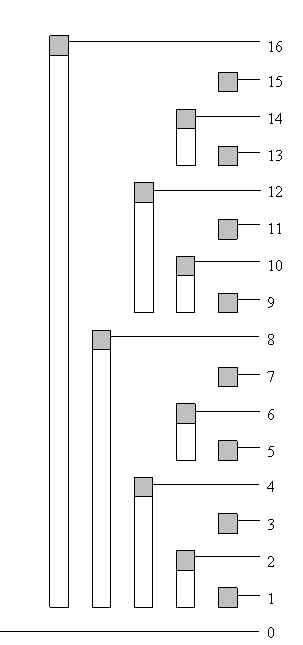
Widać, że są w pewien sposób regularne. Już teraz moglibyśmy skonstruować tablicę \( F \) off-line, np. za pomocą sum prefiksowych.

Wszystko ładnie, pięknie, ale jak można szybko znaleźć wspomniane \( lsb(x) \)? Oczywiście można to zrobić iteracyjnie, ale istnieje o wiele bardziej elegancki sposób. Przyjrzyjmy się kilku przekształceniom liczby w systemie binarnym:

\[ \begin{array}{rcll} x & = & 84_{10} & \\ & = & 0101 & 0\color{red}{1}00 \\ \sim x & = & 1010 & 1\color{red}{0}11 \\ \sim x+1 & = & 1010 & 1\color{red}{1}00 \end{array} \]

( \( \sim x \) oznacza liczbę \( x \) ze wszystkimi bitami odwróconymi)

W takim razie, łatwo można pokazać, że \( lsb(x) = x \ \& \ ( \sim x + 1) \), gdzie \( \& \) oznacza AND bitowy. Warto też zauważyć, że wyrażenie \( \sim x + 1 \) pojawia się gdzie indziej – w kodzie uzupełnień dwójkowych (U2), czyli najczęściej używanym zapisie ujemnych liczb w systemie binarnym. Jest to wyrażenie służące do policzenia negacji liczby. Tym samym, nasza ostateczna wersja to:

\[ lsb(x) = x \ \& \ -x \]

Co z łatwością przekłada się na kod C++:

template<typename T>
T lsb(T x)
{
    return x & -x;
}

Realizacja

Zapytanie

Po pierwsze zauważmy, że możemy skorzystać z założenia, że \( \circ \) jest odwracalne, i zamiast liczyć wynik na przedziale, sprowadzić zapytania do liczenia wyniku na prefiksie. Niech \( get\_prefix(i) = a_1 \circ a_2 \circ \dots \circ a_i \). Wtedy odpowiedź na zapytanie to \( get\_prefix(r) \circ get\_prefix(l-1)^\star \).

Intuicja

Sprowadziwszy problem do czegoś prostszego, przyjrzyjmy się strukturze naszego drzewa. Przyjmijmy, że szukamy wartości \( get\_prefix(i) \). Teraz bardzo ważną obserwacją jest to, że można po prostu iteracyjnie sprawdzać wartość \( F_i \) i sprowadzać problem do coraz mniejszego. Dokładniej:

\[ get\_prefix(i) = get\_prefix(i - lsb(i)) \circ F_i \]

Intuicja jest następująca: weźmy jedyny policzony przedział ktory kończy się w \( i \)-tym indeksie, dodajmy go do wyniku, i powiedzmy, że już nie pytamy o właśnie dodany przedział. Ponieważ w ten sposób zawsze będziemy otrzymywać pewien spójny przedział postaci \( \left[1, i\right] \), a w każdym indeksie kończy się dokładnie jeden przedział \( F \), to ten proces musi się zakończyć (w szczególności, na sam koniec zawsze dojdziemy do \( get\_prefix(0) = \varnothing \)).

Przykładowo, policzmy jakie \( F \) są nam potrzebne, gdy chcemy policzyć \( get\_prefix(84) \).

\[ get\_prefix(84_{10}) = get\_prefix(0101\ 0100) = \\ F_{0101\ 0\color{red}{1}00} + F_{010\color{red}{1}\ 0000} + F_{0\color{red}{1}00\ 0000} \]

A na obrazku \( get\_prefix(7) \):

Złożoność

Aby zauważyć, jaką złożoność ma takie podejście, należy przyjrzeć się reprezentacji binarnej kolejnych indeksów wykorzystywanych \( F \). Ich \( lsb \) będzie ściśle rosło, a nie może przekroczyć \( 2^{\lfloor \log_2 n \rfloor} \), więc wykonamy co najwyżej \( O(\log n) \) iteracji.

Modyfikacja

Żeby poprawnie aktualizować \( F \) po modyfikacji elementu \( a_i \), musimy wiedzieć, w jakich komórkach \( F \) policzono \( a_i \). Wtedy możemy opisać operację \( delta(i, v) \), która zmieniłaby wszystkie \( F_j \) obejmujące \( a_i \), wykonując \( F_j := F_j \circ v \).

Dzięki założeniom na temat operacji \( \circ \), jeżeli np. chcielibyśmy przypisać konkretną wartość \( b \) w \( a_i \), wykonalibyśmy \( delta(i, a_i^\star \circ b) \). W szczególności w naszym zadaniu wystarczy wykonać \( delta(i, d) \).

Prosta obserwacja

Tym razem zamiast reprezentować pewien prefiks jako sumę przedziałów \( F \), chcemy dla danego indeksu znaleźć, w jakich przedziałach \( F \) znajduje się ten indeks. Okazuje się, że zachodzi bardzo przyjemny fakt (dowód, rzecz jasna, pozostawiony jako ćwiczenie dla czytelnika):

    Wszystkie \( F_j \) zawierające w sobie indeks \( i \) mają \( j \) postaci:

\[ \begin{array}{rcl} j_1 & = & i \\ j_2 & = & i + lsb(i) = j_1 + lsb(j_1) \\ j_3 & = & i + lsb(i) + lsb(i + lsb(i)) = j_2 + lsb(j_2) \\ & \dots & \\ j_{k+1} & = & j_k + lsb(j_k) \end{array} \]

Pewne spostrzeżenie, stanowiące intuicję dla tego oczywistego faktu:

Wnioski

Ponieważ \( F \) jest długości \( n \), \( lsb \) jest dodatnie i w tym wypadku także ściśle rosnące, wysuwamy następujący wniosek: każde \( i \) zawiera się w \( O(\log n) \) przedziałach.

Wizualnie wygląda to tak, dla \( i = 5 \) oraz \( n = 16 \):

Drzewo

A gdzie obiecane drzewo? Wykonując operacje wykonywaliśmy skoki o \( lsb \) w górę (przy modyfikacji) oraz w dół (przy zapytaniu) w pewnych drzewach o wysokości \( O(\log n) \).

Drzewo zapytań

W tym drzewie rodzicem wierzchołka \( i \) jest \( i - lsb(i) \). Licząc \( get\_prefix(i) \) do wyniku dodajemy \( F_i \) oraz \( F \) wszystkich przodków \( i \) w drzewie. Każdy wierzchołek przechowuje sumę wartości z poddrzew wierzchołków na lewo od niego (czyli o mniejszym numerze) oraz o takim samym ojcu. (wierzchołek 12 przechowuje sumę 9, 10, 11).

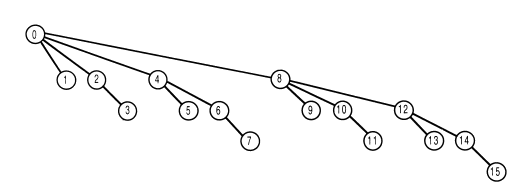
Drzewo modyfikacji

Rodzicem \( i \) jest \( i + lsb(i) \). Wykonując \( delta(i, v) \) odwiedzamy \( F_i \) oraz \( F \) wszystkich przodków \( i \). W tym drzewie każdy wierzchołek trzyma sumę indeksów wszystkich swoich potomków.

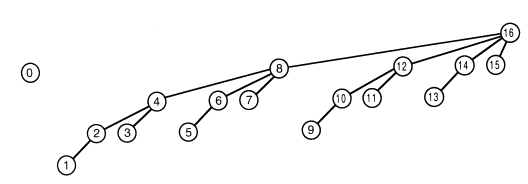
Implementacja

Wykonywane przez nas operacje były bardzo proste, dzięki czemu implementacja drzewa Fenwicka jest krótka i przyjemna. Prezentuje się tak (wykonywana operacja \( \circ \) to dodawanie, bo do tego najczęściej pisze się Fenwicka):

#include <bits/stdc++.h>

using namespace std;

template<typename T>
T lsb(T x) { return x & -x; }

template<typename T>
struct fenwick_tree
{
    size_t n;
    vector<T> F;
    fenwick_tree(size_t _n) : n(_n), F(n+1) {}
    T get_prefix(size_t i)
    {
        T r = 0;
        while(i)
            r += F[i], i -= lsb(i);
        return r;
    }
    void delta(size_t i, T v)
    {
        while(i <= n)
            F[i] += v, i += lsb(i);
    }
}

Warto wspomnieć, że generalizacja do dowolnej operacji \( \circ \) może być myląca. Na przykład powyższa implementacja nienajlepiej zadziała dla mnożenia, ponieważ \( 0 \) nie ma prawdziwej odwrotności. Jednakże, myślenie o Fenwicku jako o liczeniu operacji na pewnym spójnym podciągu może być pomocne przy zrozumieniu jego modyfikacji.

Notka o indeksowaniu od zera: w implementacjach lubię w delta dodawać i++. Wtedy można wykonywać delta tak, jak gdyby ciąg był indeksowany od zera, i uznać, że get_prefix zwraca sumę na przedziale prawostronnie otwartym \( \left[0, i\right) \). Jednak jest to kwestia gustu.

Wariacje

Fenwick, dzięki swojej prostocie, jest strukturą bardzo elastyczną i znajduje ciekawych wiele zastosowań. Ta sekcja jest poświęcona wszystkim miejscom, gdzie wcisnąłem Fenwicka tym użytecznym zastosowaniom.

Fenwick wielowymiarowy

Zaraz, zaraz. Ale kto powiedział, że \( F \) musi zawierać liczby? Możemy w nim trzymać więcej rzeczy – na przykład inne drzewa Fenwicka. Wtedy moglibyśmy obsługiwać operacje na prostokątnej tablicy \( a_{y,x} \).

Sformalizujmy to. Opiszmy drzewo Fenwicka 2D, zawierające w tablicy \( F \) drzewa Fenwicka. Wtedy \( F_i \) może zawierać drzewo Fenwicka obejmujące rzędy (\(y\)) w przedziale \( \left(i - lsb(i), i \right]\). Możemy udawać, że wtedy takie drzewo operuje na ciągu \( a' \) opisanym \( a'_{x} = \sum_{y=i-lsb(i)+1}^{i} a_{y,x} \) (rzecz jasna, zamiast sumy może być inna operacja).

Najlepsza nazwa dla tego drzewa to pewnie Fenwick po wymiarach, ponieważ można takie drzewa składać dowolnie wiele razy. Na przykład drzewo obsługujące zapytania na trójwymiarowej tablicy na indeksach \( (x, y, z) \) obsługiwałoby wszystkie indeksy trzeciego wymiaru \( z \), sprowadzając problem do dwuwymiarowego.

Implementacja jest bardzo podobna do zwykłego drzewa Fenwicka. Zakładam, że mamy dostęp do oryginalnej implementacji. Ponownie, wykonywaną operacją jest dodawanie.

template<typename T>
struct fenwick_tree_2d
{
    size_t w, h;
    vector<fenwick_tree<T>> F;
    fenwick_tree(size_t _w, size_t _h) : w(_w), h(_h), F(h+1, w) {}
    T get_prefix(size_t x, size_t y)
    {
        T r = 0;
        while(y)
            r += F.get_prefix(x), y -= lsb(y);
        return r;
    }
    void delta(size_t x, size_t y, T v)
    {
        while(y <= h)
            F[y].delta(x, v), y += lsb(y);
    }
}

Złożoność operacji \( d \)-wymiarowego Fenwicka to \( O(\log^d n) \).

Dynamiczny Fenwick

A co jeżeli chcemy obsługiwać zapytania na bardzo dużym zakresie? Zauważmy, że ponieważ każdy element występuje w \( O(\log n) \) komórkach, nie musimy trzymać ich wszystkich. Zamiast utrzymywać \( F \) w tablicy możemy skorzystać z innego kontenera, na przykład hashmapy lub BST. Możemy więc przyjąć, że dynamiczny Fenwick ma złożoność \( O(\log^2 n) \). Złożoność pamięciowa to \( O(q \log n) \), gdzie \( q \) to ilość wykonanych operacji.

Fenwick struktur

Powiedzmy, że chcemy obsługiwać na pewnej kwadratowej tablicy \( a \) (początkowo \( a_{y,x} = 0 \)) o wymiarach \( n \times n \) następujące operacje:

  1. Ustaw \( a_{y,x} \) na wartość \( 0 \) lub \( 1 \).
  2. Podaj ilość jedynek na prostokącie \( \left[1, x\right] \times \left[1, y\right] \).

Jak zwykle, zapytanie 2. jest równoważne z odpowiadaniem na zapytania na dowolnym prostokącie.

Najprościej byłoby zbudować dwuwymiarowe drzewo Fenwicka. Jednak co zrobić, jeżeli n może być duże (\( n \le 10^5 \))? Trzymając w drzewie dwuwymiarowym dynamiczne drzewa, moglibyśmy co najwyżej osiągnąć złożoność \( O(\log^3 n) \) oraz pamięciową \( O(n + q \log^2 n) \). Jednak da się lepiej.

Posłużmy się znowu tym samym pomysłem, co przy wielowymiarowym Fenwicku – przechowujmy w komórkach Fenwicka inną strukturę. Zastanówmy się teraz, jak rozwiązać ten problem w jednym wymiarze. Jednym z takich sposobów jest utrzymywanie order statistics tree (opisanego na kartce o libstdc++). Jeżeli \( a_x = 1 \), to w zbiorze znajdowałby się element \( x \). Wtedy odpowiadanie na 2. zapytanie to zwrócenie ilości elementów mniejszych od danego.

W takim razie w Fenwicku możemy utrzymywać zbiory. Gdy \( a_{y,x} = 1 \), to do zbioru wszystkich \( F \) obejmujących rząd \( y \) dodajemy element \( x \) (dla dokładności, ponieważ w zbiorze nie może być duplikatów, należałoby dodawać pary \( (x, y) \)). Liczenie ilości jedynek jest analogiczne do jednego wymiaru.

Jaką złożoność będzie miało takie podejście? Pamięciowo jest dobrze, bo możemy po prostu utrzymywać tablicę order statistics tree (czyli __gnu_pbds::tree). Każda jedynka zostanie dodana do \( O(\log n) \) zbiorów, więc sumarycznie zużyjemy \( O(n + q \log n) \) pamięci. Czasowo też jest dobrze – \( O(\log n) \) razy wykonamy operację order_of_key w czasie \( O(\log n) \) – mamy złożoność czasową \( O(\log^2 n) \).

Mikrooptymalizacje

Zapisując \( i + lsb(i) \) czy \( i - lsb(i) \) można zadać sobie pytanie, czy tego także nie da się zapisać jako operacje bitowe. Odpowiedź brzmi – owszem, da się. Okazuje się, że zachodzą takie oto własności:

\[ \begin{array}{rcl} x - lsb(x) = x - (x\ \&\ -x) & = & x\ \&\ (x - 1) \\ x + lsb(x) = x + (x\ \&\ -x) & = & (x\ |\ (x - 1)) + 1 \end{array} \]

Są to oczywiście mikrooptymalizacje i niekoniecznie dadzą nam znaczny zysk czasowy, ale gdy przepychamy rozwiązanie, może nam to trochę pomóc. W praktyce to pierwsze będzie bardziej przydatne, to drugie niekoniecznie musi przyspieszyć nasz program (ma więcej instrukcji).

Fenwick \( min \) i \( max \)

Normalnie nie moglibyśmy wykorzystać Fenwicka do liczenia \( max \). Głównym problemem jest to, że nie ma sensownej odwrotności operacji \( max \). Jednak przy konkretnych założeniach, można zbudować Fenwicka maxów.

  1. Zapytania są jedynie o prefiksy.
  2. Ustawiana wartość zawsze jest większa od poprzedniej na tym indeksie.

Założenia te działają podobnie dla \( min \). O dziwo, takie warunki czasami mamy, np. przy liczeniu dynamików.

Wyszukiwanie binarne na Fenwicku

Powiedzmy, że chcemy szukać najkrótszego prefiksu, na którym suma jest równa co najmniej pewnej wartości. Czyli chcemy znaleźć \( p_T \) spełniające:

\[ p_T = \min_i get\_prefix(i) \ge v \]

(Oczywiście przy założeniu, że wszystkie wartości w ciągu \( a \) są nieujemne)

Okazuje się, że taką operację można wykonywać w \( O(\log n) \). Posłużymy się techniką binary lifting, pojawiającą się przy LCA, czyli będzie budować wynik po potęgach 2, idąc od największych.

Utwórzmy dwie zmienne: obecny indeks prefiksu \( p = 0 \), przy którym jesteśmy (oznacza to prefiks \( \left[1, p\right] \), oraz jego sumę \( s = 0 \). Teraz przejdźmy po wszystkich potęgach dwójki \( 2^k \) dla \( k = \lfloor \log_2 n \rfloor, ..., 1, 0 \).

Będąc przy danym \( k \) sprawdźmy, czy suma na prefiksie \( p + 2^k \) przekracza poszukiwaną. Jeżeli tak, to skaczemy o \( 2^k \), czyli \( p := p + 2^k \) oraz \( s := s + F_{p+2^k} \). No właśnie, ale czy wzięta przez nas wartość \( F \) zawsze będzie poprawna? Odpowiedź brzmi tak: wynika to z tego, że idziemy od największych bitów, a długość przedziału \( F \) zależy od najmniej znaczącego bitu, który przecież wybieramy (zawsze będzie to \( k \)-ty bit).

Po przejściu po wszystkich \( k \) mamy pewność, że nie mogliśmy już o więcej zwiększyć naszej sumy nie przekraczając granicznego \( v \). W takim razie, na koniec mamy:

\[ p = \max_i get\_prefix(i) \lt v \]

Czyli poszukiwana wartość to (zwykle) \( p + 1 \). I tu uwaga: należy brać pod uwagę \( v = 0 \) i odpowiednio rozpatrywać ten przypadek. Dlatego implementacja jest napisana pod poszukiwanie tej drugiej definicji.

Implementacja jest bardzo prosta:

template<typename T>
struct fenwick_tree
{
    [...]
    size_t lower_bound(T v)
    {
        T s = 0;
        size_t p = 0;
        for(size_t k = __lg(n) + 1; k --> 0; )
            if(p + (1u << k) <= n and s + F[p + (1u << k)] < v)
                s += F[p += (1u << k)];
        return p;
    }
}

Bardzo ważnym jest zrozumieć, co dokładnie zwraca funkcja, i przetestować kilka przypadków brzegowych (dla pewności).

Statyczne order statistics tree

Za pomocą tej techniki łatwo możemy zbudować szybkie order statistics tree na wcześniej znanym zakresie wartości. Wystarczy, że zbudujemy drzewo Fenwicka zliczające wystąpienia wszystkich wartości (tak że \( a_i \) to ilość wystąpień wartości \( i \)), i szukając \( k \)-tego elementu w zbiorze odpowiednio wykorzystamy lower_bound.

Liniowa konstrukcja

Fenwicka można szybko zbudować licząc sumy prefiksowe, i licząc sumy na odpowiednich przedziałach \( F \). Ale wykorzystując taki sposób potrzebujemy dodatkowego zużycia pamięci.

Zamiast tego możemy skorzystać z interpretacji drzewowej i podać alternatywny algorytm. Konkretnie skorzystamy z drzewa modyfikacji. Mając daną tablicę \( a \) należy skopiować ją do \( F \) i dla każdego indeksu \( i = 1, 2, ..., n - 1, n \) wykonać:

\[ F_{i + lsb(i)} := F_{i + lsb(i)} + F_i \]

(O ile \( i + lsb(i) \le n \))

W ten sposób spełniamy spostrzeżoną wcześniej własność: każdy wierzchołek w drzewie modyfikacji przechowuje sumę swojego poddrzewa. Ponieważ każdy wierzchołek ma ojca o większym numerze, należy odwiedzić wierzchołki w kolejności od najmniejszego indeksu.

Zadanka

Polecam także sporą listę zadań na cp-algorithms.